Assalamualaikum Wr. Wb
Puji syukur kehadirat
Allah SWT yang telah memberikan kita kesehatan dan nikmat yang tiada tara
hingga detik ini :) Alhamdulillah kita dapat berjumpa
kembali yaa..
Pada kesempatan
kali ini kita akan sama-sama membahas tentang Aplikasi Elips, Parabola, dan Hiperbola dalam kehidupan sehari-hari. Teman-teman apakah kalian pernah mendengar dan melihat bentuk-bentuk dalam
kehidupan nyata dari Elips, Parabola, dan Hiperbola ?? Nah, untuk lebih
memahami lagi langsung simak saja yukk penjelasan dibawah ini ;)
1) ELIPS
Penerapan elips dalam kehidupan sehari-hari dapat dijumpai di
berbagai macam sektor. Pada banyak kasus, hanya beberapa informasi dalam
elips yang diketahui sehingga kita harus menentukan informasi-informasi
yang hilang untuk dapat menyelesaikan permasalahan elips yang
diberikan. Pada kasus lainnya, kita harus menulis kembali persamaan
elips yang diberikan untuk menentukan informasi yang berhubungan dengan p, q, dan f.
Contoh 1 : Permasalahan Karakteristik Elips
Di Washington D.C., terdapat taman Ellips yang terletak di antara Gedung Putih dan Monumen Washington. Taman tersebut dikelilingi oleh suatu jalan yang berbentuk elips dengan panjang sumbu mayor dan minornya secara berturut-turut adalah 458 meter dan 390 meter. Apabila pengelola taman tersebut ingin membangun air mancur pada masing-masing fokus taman tersebut, tentukan jarak antara air mancur tersebut!

Pembahasan :
Karena panjang dari sumbu mayornya 2p = 458 maka kita peroleh p = 458/2 = 229 dan p2 = 2292 = 52.441. Sedangkan panjang sumbu minornya 2q = 390, sehingga q = 390/2 = 195 dan q2 = 1952 = 38.025. Untuk menentukan f, kita dapat menggunakan persamaan fokus.

Jadi, jarak antara kedua air mancur tersebut adalah 2(120) = 240 meter.
Contoh 2 : Prosedur Medis
Litotripsi merupakan suatu prosedur medis yang dilakukan untuk menghancurkan batu di saluran kemih dengan menggunakan gelombang kejut ultrasonik sehingga pecahannya dapat dengan mudah lolos dari tubuh. Suatu alat yang disebut lithotripter, berbentuk setengah elips 3 dimensi mengaplikasikan sifat-sifat dari titik fokus elips, digunakan untuk mengumpulkan gelombang ultrasonik pada satu titik fokus untuk dikirimkan ke batu ginjal yang terletak di titik fokus lainnya. Perhatikan gambar berikut.

Jika lithotripter tersebut memiliki panjang (sumbu semi mayor) 16 cm dan berjari-jari (sumbu semi minor) 10 cm, seberapa jauh dari titik puncak seharusnya batu ginjal tersebut diposisikan agar diperoleh hasil yang maksimal?
Pembahasan :
Dari soal, kita dapatkan panjang sumbu semi mayornya adalah q = 16, sehingga q2 = 162 = 256 dan panjang sumbu semi minornya adalah p = 10, sehingga p2 = 102 = 100. Dengan menggunakan persamaan fokus,

Sehingga, jarak titik puncak dengan titik fokus di mana batu ginjal diposisikan dapat ditentukan sebagai berikut.

Jadi, agar diperoleh hasil yang maksimal, batu ginjal tersebut seharusnya terletak pada jarak 28,49 dari titik puncak lithotripter.
2) PARABOLA
Seperti pada elips dan hiperbola, banyak sekali aplikasi parabola yang bertumpu pada definisi analitisnya daripada bentuk aljabarnya. Aplikasi-aplikasi tersebut, misalkan pembangunan teleskop radio dan perusahaan lampu senter, menggunakan definisi analitis parabola dalam penentuan lokasi fokus dari parabola tersebut. Berikut ini definisi analitis dari suatu parabola.
Contoh 1 : Menentukan Fokus dan Direktriks dari suatu Parabola
Tentukan titik puncak, fokus, dan direktris dari parabola yang didefinisikan oleh persamaan x² = –12y. Kemudian gambarkan grafiknya, disertai dengan fokus dan direktrisnya.
Pembahasan :
Karena hanya suku-x yang dikuadratkan dan tidak ada pergeseran yang diterapkan, maka parabola tersebut merupakan parabola vertikal dengan titik puncak di (0, 0). Dengan membandingkan persamaan yang diberikan dengan persamaan umum parabola bentuk fokus-direktriks kita dapat menentukan nilai p:

Karena p = –3 (p < 0), maka parabola tersebut terbuka ke bawah, dengan titik fokus di (0, –3) dan direktriksnya y = 3. Untuk menggambar grafiknya, kita perlu beberapa titik tambahan yang dilalui oleh parabola tersebut. Karena 36 = 6² dapat dibagi oleh 12, maka kita dapat mensubstitusikan x = 6 dan x = –6, dan menghasilkan titik-titik (6, –3) dan (–6, –3). Sehingga grafik dari parabola tersebut dapat digambarkan sebagai berikut.

Dari grafik di atas, kita dapat mengetahui bahwa garis x = 0 merupakan sumbu simetri dari grafik parabola yang diberikan.
Sebagai titik-titik alternatif dalam menggambar grafik parabola, kita dapat menggunakan apa yang disebut tali busur fokus dari parabola. Serupa dengan elips dan hiperbola, tali busur fokus adalah ruas garis yang melalui fokus, sejajar dengan direktriks, dan titik-titik ujungnya terletak pada grafik. Dengan menggunakan definisi dari parabola, jarak horizontal dari f ke (x, y) adalah 2p. Karena d1 = d2, maka ruas garis yang sejajar dengan direktriks dari fokus ke grafik memiliki panjang |2p|, dan panjang tali busur fokus dari sembarang parabola adalah |4p|.
Dan akhirnya, jika titik puncak dari suatu parabola vertikal digeser ke (h, k), maka persamaan dari parabola tersebut akan menjadi (x ± h)2 = 4p(y ± k). Seperti pada keluarga irisan kerucut lainnya, pergeseran vertikal dan horizontalnya berlawanan dengan tandanya (positif atau negatif).
Contoh 2 : Menentukan Persamaan dari suatu Parabola
Tentukan persamaan dari parabola yang memiliki titik puncak (4, 4) dan fokus (4, 1). Kemudian gambarkan grafiknya dengan menggunakan persamaan dan tali busur fokusnya.
Pembahasan :
Karena titik puncak dan fokusnya terletak pada garis vertikal, maka parabola yang dimaksud merupakan suatu parabola vertikal yang memiliki persamaan umum (x ± h)² = 4p(y ± k). Jarak p dari fokus ke titik pusat adalah 3 satuan, dan karena fokus berada di bawah titik puncak, maka grafiknya terbuka ke bawah dan p = –3. Dengan menggunakan tali busur fokus, jarak horizontal dari fokus ke grafik adalah |2p| = |2(–3)| = 6, memberikan titik-titik (–2, 1) dan (10, 1). Titik puncaknya digeser 4 satuan ke kanan dan 4 satuan ke atas dari (0, 0), sehingga diperoleh h = 4 dan k = 4. Sehingga persamaan dari parabola tersebut adalah (x – 4)² = –12(y – 4), dengan direktriks y = 7. Grafik dari parabola tersebut dapat digambarkan sebagai berikut.
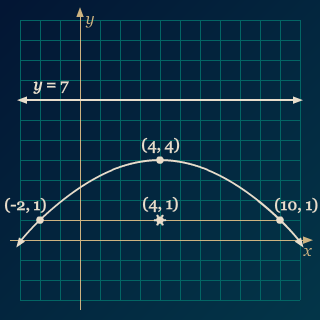
Perhatikan bahwa grafik parabola di atas memiliki sumbu simetri di garis x = 4.
3) HIPERBOLA
Permasalahan yang melibatkan fokus suatu hiperbola banyak kita jumpai di berbagai bidang. Seperti permasalahan fokus pada elips, hanya beberapa informasi hiperbola yang nantinya akan diketahui. Untuk itu, kita harus memanipulasi persamaan hiperbola yang diberikan atau bahkan membangun persamaan hiperbola dari suatu informasi tertentu untuk menentukan selesaian yang diberikan.
Contoh 1 : Menerapkan Karakteristik Hiperbola—Lintasan dari Suatu Komet
Komet-komet yang memiliki kecepatan yang sangat tinggi tidak dapat dipengaruhi oleh gravitasi matahari, dan akan mengitari matahari dengan lintasan berbentuk hiperbola dengan matahari sebagai salah satu titik fokusnya. Jika lintasan komet yang diilustrasikan oleh gambar di bawah dapat dimodelkan oleh persamaan 2.116x2 – 400y2 = 846.400, seberapa dekatkah komet tersebut dengan matahari? Anggap satuannya dalam jutaan mil.
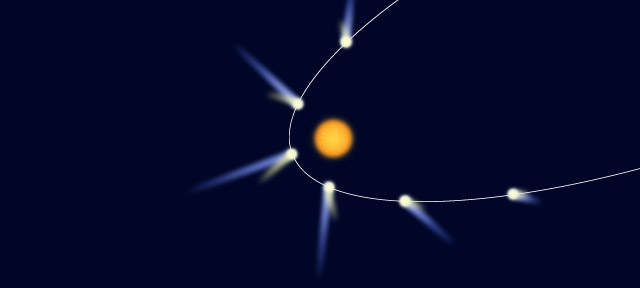
Pembahasan :
Pada dasarnya, dalam permasalahan ini kita diminta untuk menentukan jarak antara fokus dengan titik puncak hiperbola. Dengan menuliskan persamaan yang diberikan ke dalam bentuk standar,
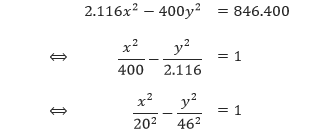
Sehingga, kita peroleh p = 20 (p2 = 400) dan q = 46 (q2 = 2.116). Dengan menggunakan persamaan fokus untuk menentukan f dan f2, kita mendapatkan,

Karena p = 20 dan |f| = 50, jarak komet tersebut dengan matahari adalah 50 – 20 = 30 juta mil atau sekitar 4,83 × 107 kilometer.
Contoh 2 : Lokasi dari Suatu Badai
Dua orang ahli meteorologi melihat badai dari tempat mereka tinggal. Tempat tinggal dua orang ahli meteorologi tersebut berjarak 4 km (4.000 m). Ahli meteorologi pertama, yang jaraknya lebih jauh dari badai, mendengar suara petir 9 detik setelah ahli meteorologi kedua. Jika kecepatan suara 340 m/s, tentukan persamaan yang dapat memodelkan lokasi dari badai tersebut.

Pembahasan :
Misalkan M1 merupakan ahli meteorologi pertama dan M2 merupakan ahli meteorologi kedua. Karena M1 mendengar petir 9 detik setelah M2, maka lokasi M1, 9 ∙ 340 = 3.060 m lebih jauh dari M1 terhadap lokasi badai. Atau apabila disimbolkan, |M1S| – |M2S| = 3.060. Himpunan semua titik S yang sesuai dengan persamaan ini akan membentuk suatu grafik hiperbola, dan kita akan menggunakan fakta ini untuk membangun suatu persamaan yang memodelkan semua kemungkinan dari lokasi badai tersebut. Selanjutnya, mari kita gambar informasi-informasi di atas pada koordinat Cartesius sehingga M1 dan M2 terletak pada sumbu-x dan titik asal (0, 0) kita buat sebagai pusatnya.

Dengan selisih konstannya 3.060, kita mendapatkan 2p = 3.060 sehingga p = 1.530. Karena jarak antara M1 dan M2 adalah 4.000, maka jarak antara pusat dengan M1 atau M2 adalah f = 1/2 ∙ 4.000 = 2.000. Dengan menggunakan persamaan fokus, kita mendapatkan

Sehingga, persamaan lokasi dari badai tersebut adalah
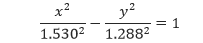
Terimakasih, semoga bermanfaat :)
Wassalamualaikum Wr. Wb
Sumber :
https://yos3prens.wordpress.com/2014/01/17/5-soal-dan-pembahasan-penerapan-elips/
https://yos3prens.wordpress.com/2014/05/19/persamaan-parabola/
https://yos3prens.wordpress.com/2014/01/29/5-soal-dan-pembahasan-permasalahan-fokus-suatu-hiperbola/
Contoh 1 : Permasalahan Karakteristik Elips
Di Washington D.C., terdapat taman Ellips yang terletak di antara Gedung Putih dan Monumen Washington. Taman tersebut dikelilingi oleh suatu jalan yang berbentuk elips dengan panjang sumbu mayor dan minornya secara berturut-turut adalah 458 meter dan 390 meter. Apabila pengelola taman tersebut ingin membangun air mancur pada masing-masing fokus taman tersebut, tentukan jarak antara air mancur tersebut!

Pembahasan :
Karena panjang dari sumbu mayornya 2p = 458 maka kita peroleh p = 458/2 = 229 dan p2 = 2292 = 52.441. Sedangkan panjang sumbu minornya 2q = 390, sehingga q = 390/2 = 195 dan q2 = 1952 = 38.025. Untuk menentukan f, kita dapat menggunakan persamaan fokus.

Jadi, jarak antara kedua air mancur tersebut adalah 2(120) = 240 meter.
Contoh 2 : Prosedur Medis
Litotripsi merupakan suatu prosedur medis yang dilakukan untuk menghancurkan batu di saluran kemih dengan menggunakan gelombang kejut ultrasonik sehingga pecahannya dapat dengan mudah lolos dari tubuh. Suatu alat yang disebut lithotripter, berbentuk setengah elips 3 dimensi mengaplikasikan sifat-sifat dari titik fokus elips, digunakan untuk mengumpulkan gelombang ultrasonik pada satu titik fokus untuk dikirimkan ke batu ginjal yang terletak di titik fokus lainnya. Perhatikan gambar berikut.

Jika lithotripter tersebut memiliki panjang (sumbu semi mayor) 16 cm dan berjari-jari (sumbu semi minor) 10 cm, seberapa jauh dari titik puncak seharusnya batu ginjal tersebut diposisikan agar diperoleh hasil yang maksimal?
Pembahasan :
Dari soal, kita dapatkan panjang sumbu semi mayornya adalah q = 16, sehingga q2 = 162 = 256 dan panjang sumbu semi minornya adalah p = 10, sehingga p2 = 102 = 100. Dengan menggunakan persamaan fokus,

Sehingga, jarak titik puncak dengan titik fokus di mana batu ginjal diposisikan dapat ditentukan sebagai berikut.

Jadi, agar diperoleh hasil yang maksimal, batu ginjal tersebut seharusnya terletak pada jarak 28,49 dari titik puncak lithotripter.
2) PARABOLA
Seperti pada elips dan hiperbola, banyak sekali aplikasi parabola yang bertumpu pada definisi analitisnya daripada bentuk aljabarnya. Aplikasi-aplikasi tersebut, misalkan pembangunan teleskop radio dan perusahaan lampu senter, menggunakan definisi analitis parabola dalam penentuan lokasi fokus dari parabola tersebut. Berikut ini definisi analitis dari suatu parabola.
Contoh 1 : Menentukan Fokus dan Direktriks dari suatu Parabola
Tentukan titik puncak, fokus, dan direktris dari parabola yang didefinisikan oleh persamaan x² = –12y. Kemudian gambarkan grafiknya, disertai dengan fokus dan direktrisnya.
Pembahasan :
Karena hanya suku-x yang dikuadratkan dan tidak ada pergeseran yang diterapkan, maka parabola tersebut merupakan parabola vertikal dengan titik puncak di (0, 0). Dengan membandingkan persamaan yang diberikan dengan persamaan umum parabola bentuk fokus-direktriks kita dapat menentukan nilai p:

Karena p = –3 (p < 0), maka parabola tersebut terbuka ke bawah, dengan titik fokus di (0, –3) dan direktriksnya y = 3. Untuk menggambar grafiknya, kita perlu beberapa titik tambahan yang dilalui oleh parabola tersebut. Karena 36 = 6² dapat dibagi oleh 12, maka kita dapat mensubstitusikan x = 6 dan x = –6, dan menghasilkan titik-titik (6, –3) dan (–6, –3). Sehingga grafik dari parabola tersebut dapat digambarkan sebagai berikut.

Dari grafik di atas, kita dapat mengetahui bahwa garis x = 0 merupakan sumbu simetri dari grafik parabola yang diberikan.
Sebagai titik-titik alternatif dalam menggambar grafik parabola, kita dapat menggunakan apa yang disebut tali busur fokus dari parabola. Serupa dengan elips dan hiperbola, tali busur fokus adalah ruas garis yang melalui fokus, sejajar dengan direktriks, dan titik-titik ujungnya terletak pada grafik. Dengan menggunakan definisi dari parabola, jarak horizontal dari f ke (x, y) adalah 2p. Karena d1 = d2, maka ruas garis yang sejajar dengan direktriks dari fokus ke grafik memiliki panjang |2p|, dan panjang tali busur fokus dari sembarang parabola adalah |4p|.
Dan akhirnya, jika titik puncak dari suatu parabola vertikal digeser ke (h, k), maka persamaan dari parabola tersebut akan menjadi (x ± h)2 = 4p(y ± k). Seperti pada keluarga irisan kerucut lainnya, pergeseran vertikal dan horizontalnya berlawanan dengan tandanya (positif atau negatif).
Contoh 2 : Menentukan Persamaan dari suatu Parabola
Tentukan persamaan dari parabola yang memiliki titik puncak (4, 4) dan fokus (4, 1). Kemudian gambarkan grafiknya dengan menggunakan persamaan dan tali busur fokusnya.
Pembahasan :
Karena titik puncak dan fokusnya terletak pada garis vertikal, maka parabola yang dimaksud merupakan suatu parabola vertikal yang memiliki persamaan umum (x ± h)² = 4p(y ± k). Jarak p dari fokus ke titik pusat adalah 3 satuan, dan karena fokus berada di bawah titik puncak, maka grafiknya terbuka ke bawah dan p = –3. Dengan menggunakan tali busur fokus, jarak horizontal dari fokus ke grafik adalah |2p| = |2(–3)| = 6, memberikan titik-titik (–2, 1) dan (10, 1). Titik puncaknya digeser 4 satuan ke kanan dan 4 satuan ke atas dari (0, 0), sehingga diperoleh h = 4 dan k = 4. Sehingga persamaan dari parabola tersebut adalah (x – 4)² = –12(y – 4), dengan direktriks y = 7. Grafik dari parabola tersebut dapat digambarkan sebagai berikut.

Perhatikan bahwa grafik parabola di atas memiliki sumbu simetri di garis x = 4.
3) HIPERBOLA
Permasalahan yang melibatkan fokus suatu hiperbola banyak kita jumpai di berbagai bidang. Seperti permasalahan fokus pada elips, hanya beberapa informasi hiperbola yang nantinya akan diketahui. Untuk itu, kita harus memanipulasi persamaan hiperbola yang diberikan atau bahkan membangun persamaan hiperbola dari suatu informasi tertentu untuk menentukan selesaian yang diberikan.
Contoh 1 : Menerapkan Karakteristik Hiperbola—Lintasan dari Suatu Komet
Komet-komet yang memiliki kecepatan yang sangat tinggi tidak dapat dipengaruhi oleh gravitasi matahari, dan akan mengitari matahari dengan lintasan berbentuk hiperbola dengan matahari sebagai salah satu titik fokusnya. Jika lintasan komet yang diilustrasikan oleh gambar di bawah dapat dimodelkan oleh persamaan 2.116x2 – 400y2 = 846.400, seberapa dekatkah komet tersebut dengan matahari? Anggap satuannya dalam jutaan mil.

Pembahasan :
Pada dasarnya, dalam permasalahan ini kita diminta untuk menentukan jarak antara fokus dengan titik puncak hiperbola. Dengan menuliskan persamaan yang diberikan ke dalam bentuk standar,
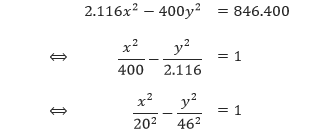
Sehingga, kita peroleh p = 20 (p2 = 400) dan q = 46 (q2 = 2.116). Dengan menggunakan persamaan fokus untuk menentukan f dan f2, kita mendapatkan,

Karena p = 20 dan |f| = 50, jarak komet tersebut dengan matahari adalah 50 – 20 = 30 juta mil atau sekitar 4,83 × 107 kilometer.
Contoh 2 : Lokasi dari Suatu Badai
Dua orang ahli meteorologi melihat badai dari tempat mereka tinggal. Tempat tinggal dua orang ahli meteorologi tersebut berjarak 4 km (4.000 m). Ahli meteorologi pertama, yang jaraknya lebih jauh dari badai, mendengar suara petir 9 detik setelah ahli meteorologi kedua. Jika kecepatan suara 340 m/s, tentukan persamaan yang dapat memodelkan lokasi dari badai tersebut.

Pembahasan :
Misalkan M1 merupakan ahli meteorologi pertama dan M2 merupakan ahli meteorologi kedua. Karena M1 mendengar petir 9 detik setelah M2, maka lokasi M1, 9 ∙ 340 = 3.060 m lebih jauh dari M1 terhadap lokasi badai. Atau apabila disimbolkan, |M1S| – |M2S| = 3.060. Himpunan semua titik S yang sesuai dengan persamaan ini akan membentuk suatu grafik hiperbola, dan kita akan menggunakan fakta ini untuk membangun suatu persamaan yang memodelkan semua kemungkinan dari lokasi badai tersebut. Selanjutnya, mari kita gambar informasi-informasi di atas pada koordinat Cartesius sehingga M1 dan M2 terletak pada sumbu-x dan titik asal (0, 0) kita buat sebagai pusatnya.

Dengan selisih konstannya 3.060, kita mendapatkan 2p = 3.060 sehingga p = 1.530. Karena jarak antara M1 dan M2 adalah 4.000, maka jarak antara pusat dengan M1 atau M2 adalah f = 1/2 ∙ 4.000 = 2.000. Dengan menggunakan persamaan fokus, kita mendapatkan

Sehingga, persamaan lokasi dari badai tersebut adalah
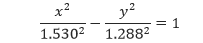
Terimakasih, semoga bermanfaat :)
Wassalamualaikum Wr. Wb
Sumber :
https://yos3prens.wordpress.com/2014/01/17/5-soal-dan-pembahasan-penerapan-elips/
https://yos3prens.wordpress.com/2014/05/19/persamaan-parabola/
https://yos3prens.wordpress.com/2014/01/29/5-soal-dan-pembahasan-permasalahan-fokus-suatu-hiperbola/

Makasih
BalasHapus